Cyclotomic Fields and LatticeFold
You can go far as a ZK dev without any formal training in abstract or linear algebra. I managed to understand STARKs, pairings, plonk, KZG, and even folding schemes from a software engineering angle, without needing to dive too deep into algebra topics. However, to understand LatticeFold, this has not been the case.
Why study LatticeFold?
I am obsessed with succinct blockchains, ever since stumbling upon Mina several years ago, and my motivation for learning ZK is mainly centered around improving this construction as much as possible. I dream of a high TPS succinct blockchain, with instant-syncing light nodes and data availability verification. This is the white whale I have chased for years now.
While STARKs dominate the modern zk proof landscape thanks to small fields and GPU-friendliness, you can’t ignore the potential of folding schemes when focusing on succinct blockchains as the use-case. Mina itself uses HALO accumulation, which can be viewed in this context as an older, more-primitive equivalent of folding schemes.
Limitations of Folding Schemes
As discussed in Liam’s talk at ZuBerlin, folding schemes have not been widely adopted. Part of the reasons given for this are the commitment costs associated with curve-based commitment schemes due to large fields, and the need to “keep the witness around” when doing distributed proving.
The former makes sense- it’s entirely possible that a succinct blockchain built using STARK recursion might actually be faster, since the proofs can be computed so much faster thanks to hardware friendliness. However, the second point does not apply since it’s a different use-case.
I’ll argue the real reason folding schemes haven’t been adopted is because… in the grand scheme of things, ZK is a pretty small scene. Not every team has a good use-case for folding, and they have already married different approaches like STARKs. Not that many people are building in this space. They’re still pretty new, it’s going to take some time.
Does LaticeFold overcome these limitations?
The high commitment cost of using curve-based proof system is no joke, but there’s a chance lattices might offer a solution. The fields used in Lattice cryptography are smaller than elliptic curve fields. In Nethermind’s LatticeFold codebase, we see cyclotomic fields constructed over BabyBear (a 32-bit GPU-friendly field).
Some overhead is incurred because they’re not as simple as the prime fields used in STARKs. Cyclotomic fields are complex numbers with multiple components, so performing arithmetic operations on them is more like vector operations than integer operations. Still, it certainly seems like there is a chance they might be more hardware-friendly and practical than other folding schemes, and it’s worth determining this experimentally to see if this gives us the sweet spot between folding’s cheap recursion, and the hardware friendliness of STARKs.
Cyclotomic Fields
The SNARK and STARK schemes you’re familiar with are probably using prime fields, or perhaps extension fields if you’re particularly deep in the weeds (see vitalik’s Binius explainer which touches on this concept).
The Lattice-based schemes tend to use Cyclotomic Fields, which are a different kind of field. If I understand correctly, this means the circuits for these proofs sytemes need to be written with their variables and constraints in cyclotomic fields, rather than the kind we are used to, which means we can’t use any existing ZK circuit tooling, and devs might have to be aware of some new concepts.
For this reason, I began to dive into algebra to understand how these things work, so I might be able to develop a circuit for these proof systems when the time comes.
Why Cyclotomic Fields?
While many snarks, digital signatures, and encryption are based on the computational hardness of the discrete log problem, Lattice constructions are based on a different class of computationally hard problem, called Short Integer Solution (SIS) problems.
According to the Wikipedia page, there are different variants of the SIS problem, notably the Ring SIS (“R-SIS”) and Module SIS (“M-SIS”) problems, which deal with Cyclotomic fields / rings.

LatticeFold references the M-SIS problem and seems to be constructed on-top of it.
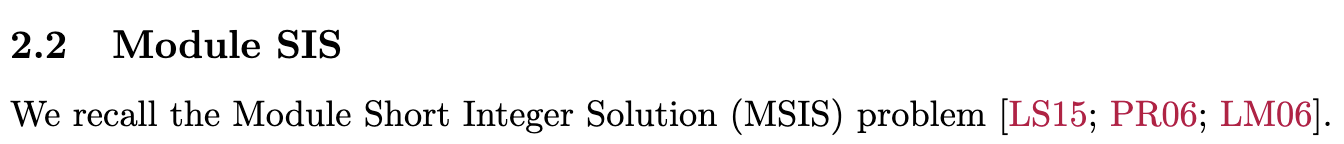
Additionally, we can see many of the codebases related to latticefold and Ajtai contain code for cyclotomic fields / rings, like from Nethermind and Autoparallel.
Not your grandma’s numbers
While extension fields and cyclotomic fields are polynomials, not numbers, they do behave like numbers in a lot of very important ways!
They can be added, multiplied, subtracted, divided, and there is still a notion of “one” and “zero”, called multiplicative and additive identities, respectively. It turns out, this is all you need to develop circuits for useful statements.
Stay tuned as I dive further into this and maybe I will write a more-formal explainer as I learn more.
A note on data availability and succinct blockchains
If data availability verification is a design goal for the idealized succinct blockcahin, then one might infer that ZODA and The Accidental Computer are the best known ways to prove and verify the chain. Does that change anything?
Not really. While GKR proves statements over “depth-2 arithmetic circuits”, if your goal is to include a proof of the previous block’s validity in the statement for the current block, folding schemes might still be the best way to do it! So folding is still relevant even in the world of interactive proofs.
